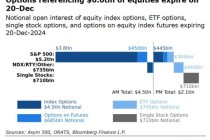
期权费用的计算方法
在期货市场中,期权是一种重要的金融衍生品,它赋予持有者在未来某一特定时间内以特定费用 买入或卖出一定数量的标的资产的权利,而非义务。期权费用,也称为期权费用 或期权溢价,是购买这一权利的成本。了解期权费用的计算方法对于投资者来说至关重要,因为它直接影响到投资决策和风险管理。
期权费用的计算涉及多个因素,主要包括以下几个方面:
因素 描述 标的资产费用 期权所关联的标的资产的当前市场费用 。 行权费用 期权持有者可以买入或卖出标的资产的预定费用 。 到期时间 期权有效的剩余时间,时间越长,期权价值通常越高。 波动率 标的资产费用 波动的预期程度,波动率越高,期权价值越高。 无风险利率 市场上的无风险投资收益率,影响期权的时间价值。 股息率 如果标的资产是股票,股息率也会影响期权费用 。期权费用的计算通常使用布莱克-斯科尔斯模型(Black-Scholes Model)或其他类似的定价模型。这些模型通过数学公式来估算期权的费用 ,考虑了上述所有因素。布莱克-斯科尔斯模型的基本公式如下:
\[ C = S \cdot N(d_1) - X \cdot e^{-rT} \cdot N(d_2) \]
其中:
\( C \) 是看涨期权的费用 \( S \) 是标的资产的当前费用 \( X \) 是期权的行权费用 \( r \) 是无风险利率 \( T \) 是期权的到期时间 \( N(d) \) 是标准正态分布的累积分布函数 \( d_1 \) 和 \( d_2 \) 是根据模型计算出的中间变量对于看跌期权,其费用 可以通过看涨期权费用 和标的资产费用 之间的关系来推导。
投资者在使用这些模型时需要注意,虽然布莱克-斯科尔斯模型是一个广泛接受的理论模型,但在实际应用中,市场条件和模型假设之间可能存在差异,因此实际的期权费用 可能会与模型计算的结果有所不同。此外,期权交易还需要考虑交易成本、税收和其他市场因素。
总之,期权费用的计算是一个复杂的过程,涉及多个变量和假设。投资者在参与期权交易前,应充分了解这些计算方法,并结合自身的投资策略和风险承受能力,做出明智的投资决策。






发表评论